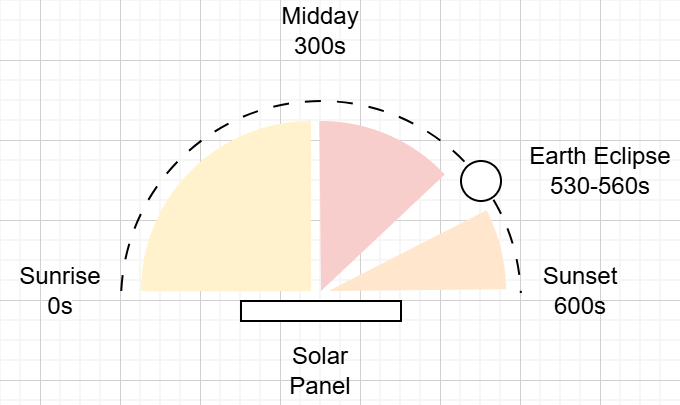
Estimating Solar Panel Efficiency

This guide explores how solar panel tilt and tracking impact power efficiency on the Moon in Stationeers.

Introduction

Reliable power is essential for lunar operations, but solar panel output varies with the Moon’s day-night cycle, eclipses, and panel alignment. As bases expand, understanding solar efficiency becomes vital for capacity planning.

This guide analyzes static and tracking solar panels on the Moon. It introduces key orbital parameters, models solar output across configurations, and offers strategies to optimize power production for long-term reliability.

Lunar Solar Parameters

• Cycle Period: 20 minutes

• Solar Orbit Time: 20.3 minutes

• Solar Power Range: 1315-1407 W/m²

• Eclipse Range: 159°-168°

Simplifying Assumptions

• Horizontal angle changes have negligible impact.

• Solar panels capture energy once per second.

• Power remains within defined limits even near the horizon or eclipse edges.

• Efficiency scales linearly with perpendicular solar alignment.

• No terrain or structures block sunlight.

Static Horizontal Panel (Baseline)

The baseline model assumes a flat solar panel lying on the lunar surface:

Solar trajectory across a horizontal solar panel.

Power Calculation

At lunar noon (300s), the panel reaches its peak output of 500 W. This defines the efficiency ratio, representing the rate of power increase per second:

\(\text{Efficiency Ratio} = \frac{\text{Max Power}}{\text{Time to Noon}} = \frac{500 \ \text{W}}{300 \ \text{s}} = \frac{5}{3} \ \text{W/s}\)

To capture the symmetric rise and fall of solar power, time is normalized around lunar noon:

\(t' = \begin{cases} t, & t \lt 300 \\ 600 - t, & t \geq 300 \end{cases}\)

And instantaneous power is then:

\(P(t') = \frac{5}{3} \times t'\)

Shown in the graph below, this creates a triangular power curve centered at noon, with a brief dip during the Earth eclipse (530–560 s).

Energy Calculation

Energy is computed by summing the power at each second of the day. For a time segment [t_start, t_end), the energy is:

\(E = (t_\text{end} - t_\text{start}) \times \frac{P(t'_\text{start}) + P(t'_{\text{end}-1})}{2}\)

Where P(t') = ⁵/₃ × t', and

• t' = t when t < 300

• t' = 600 - t when t ≥ 300

To calculate total energy, subdivide the problem into time segments that consider rise and fall periods and the eclipse:

Segment Calculations

• Sunrise to Midday [0, 300)

  \(\begin{align} t'_{\text{start}} &= 0 \\ t'_{\text{end}-1} &= 299 \\ E &= (300 - 0) \times \frac{P(0) + P(299)}{2} \\ &= 300 \times \frac{0 + 498.\overline{3}}{2} \\ &= 74,750\ \text{J} \end{align} \)

• Noon to Eclipse Start [300, 530)

  \(\begin{align} t'_{\text{start}} &= 600 - 300 = 300 \\ t'_{\text{end}-1} &= 600 - 529 = 71 \\ E &= (530 - 300) \times \frac{P(300) + P(71)}{2} \\ &= 230 \times \frac{500 + 118.\overline{3}}{2} \\ &= 71,108.\overline{3}\ \text{J} \end{align}\)

• Eclipse End to Sunset (560, 600)

  \(\begin{align} t'_{\text{start}} &= 600 - 560 = 40 \\ t'_{\text{end}-1} &= 600 - 599 = 1 \\ E &= (600 - 560) \times \frac{P(40) + P(1)}{2} \\ &= 40 \times \frac{66.\overline{6} + 1.\overline{6}}{2} \\ &= 1,300\ \text{J} \end{align}\)

Total energy: ~147158.3 J

Static Tilt Panel

Tilting a panel changes the timing of peak sunlight exposure, enabling better alignment with morning or afternoon light. This section extends the horizontal model by introducing angular offsets and shifting the power curve accordingly.

Characteristics

• The sun moves 180° over 600 seconds, or 0.3° per second.

• A panel tilted by θ° reaches peak output when the sun is at that same angle.

• Tilt range: −90° (faces sunrise) to +90° (faces sunset)

Time-Angle Mapping

A tilt angle θ offsets the peak output time:

\(\begin{align} \text{offset} &= \frac{\theta}{0.3} \\ t_{\text{mid}} &= 300 + \text{offset} \\ \end{align}\)

Adjusting daylight bounds to:

\(\begin{align} t_{\text{min}} &= \max(\text{offset}, 0) \\ t_{\text{max}} &= \min(600 + \text{offset}, 600) \\ \end{align}\)

Time Normalization

To reuse the triangular power model, normalize time around the new midpoint:

\(\begin{align} \text{offset} &= \frac{\theta}{0.3} \\ P(t') = \frac{5}{3} \times t' \ \text{with} \ t' &= \begin{cases} t-\text{offset}, & t \lt 300 + \text{offset}\\ 600 - (t - \text{offset}), & t \geq 300 + \text{offset} \end{cases} \end{align}\)

Allowing the energy model to remain unchanged for any segment:

\(E = (t_\text{end} - t_\text{start}) \times \frac{P(t'_\text{start}) + P(t'_{\text{end}-1})}{2}\)

Example: -45° Tilt

A panel tilted -45° faces the morning sun, achieving peak exposure earlier in the day. Using the formulas introduced above:

\(\begin{align} \text{offset} &= \frac{-45}{0.3} = -150 \\ t_{\text{min}} &= \max(-150, 0) = 0 \\ t_{\text{mid}} &= 300 + (-150) = 150 \\ t_{\text{max}} &= \min(600 + (-150), 600) = 450 \\ \end{align}\)

Yields two segments as illustrated in the diagram:

• Morning rise: t = 0 to t = 150

• Afternoon fall: t = 150 to t = 450

Segment Calculations

• Sunrise to Mid [0, 150):

\(\begin{align} t'_{\text{start}} &= 0 - (-150) = 150\\ t'_{\text{end}-1} &= 150 - 1 - (-150) = 299 \\ E_1 &= (150 - 0) \times \frac{P(150) + P(299)}{2} \\ &= 150 \times \frac{250 + 498.\overline{3}}{2} \\ &= 56,125\ \text{J} \end{align}\)

• Mid to Max [150, 450):

\(\begin{align} t'_{\text{start}} &= 600 - (150 - (-150)) = 300\\ t'_{\text{end}-1} &= 600 - (450 - 1 - (-150)) = 1 \\ E_2 &= (450 - 150) \times \frac{P(300) + P(1)}{2} \\ &= 300 \times \frac{500 + 1.\overline{6}}{2} \\ &= 75,250\ \text{J} \end{align}\)

Total Energy: 131,375 J

Tracking Panel

Tracking panels maintain near-perpendicular alignment with the sun, boosting energy capture.

Characteristics

• Can be programmed to rotate and maintain perpendicular alignment with the sun.

• Are limited to a 150° sweep and cannot track near the horizon.

• Have reduced output from 0-50s and 550-600s due to the limitation in their tracking ability.

Segment Calculations

The energy segments of a tracking solar panel include the time from sunrise to track start, track start to eclipse start, and eclipse end to sunset:

• Sunrise to Track Start [0, 50)

  Treated like a static panel tilted -75°

  \(\begin{align} \text{offset} &= \frac{-75}{0.3} = -250 \\ t'_{\text{start}} &= (0 - (-250)) = 250 \\ t'_{\text{end}-1} &= 50 - 1 - (-250) = 299 \\ E_1 &= (50 - 0) \times \frac{P(250) + P(299)}{2} \\ &= 50 \times \frac{416.\overline{6} + 498.\overline{3}}{2} \\ &= 22,875\ \text{J} \end{align}\)

• Track Start to Eclipse Start [50, 530)

  Full tracking at 500 W

  \(E_2 = (530 - 50) \times 500 = 480 \times 500 = 240,000\ \text{J} \)

• Eclipse End to Sunset [560, 600)

  Treated like a static panel tilted 75°

  \(\begin{align} \text{offset} &= \frac{75}{0.3} = 250 \\ t'_{\text{start}} &= 600 - (560 - 250) = 290 \\ t'_{\text{end}-1} &= 600 - ((600 - 1 - 250) = 251 \\ E_3 &= (600 - 560) \times \frac{P(290) + P(251)}{2} \\ &= 40 \times \frac{483.\overline{3} + 418.\overline{3}}{2} \\ &= 18,033.\overline{3}\ \text{J} \end{align}\)

Total Energy: ~280,908.3 J

Power Production Summary

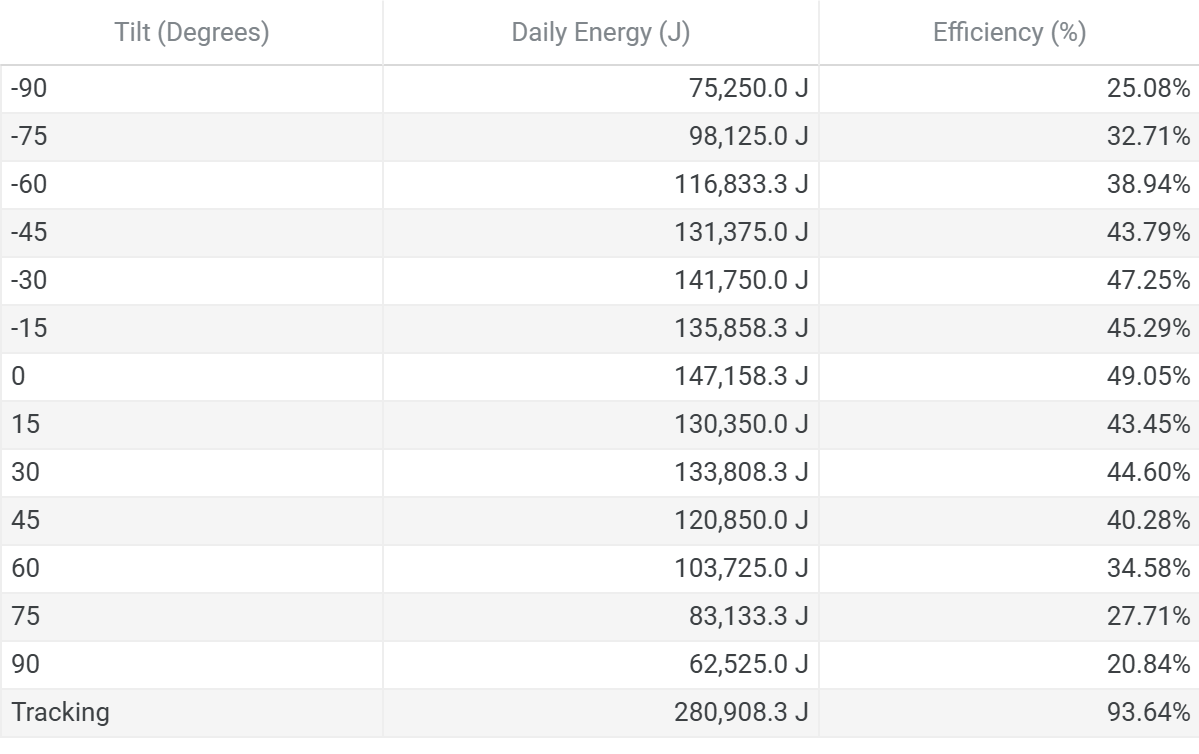
The table below summarizes daily energy output and efficiency for various panel tilts. Efficiency is calculated as the ratio of actual energy collected to the theoretical maximum of 300,000 J (500 W × 600 s).

Key insights:

• Flat panels (0° tilt) maximize energy collection due to symmetrical solar exposure.

• Tilting shifts peak energy earlier or later but reduces total output.

• Tracking panels nearly double energy yield by maintaining optimal alignment.

Conclusion

Effective lunar solar power relies on strategic panel alignment and understanding the sun’s movement. While static panels achieve up to 50% efficiency when well-oriented, tracking panels significantly boost energy capture by maintaining optimal sun alignment. Applying these models helps design scalable, reliable power systems to meet growing lunar base demands.

---

Content structure and technical calculations were enhanced with support from AI tools (ChatGPT).